Métodos de Regresión

Regresión se refiere a la aproximación del valor real de la función que determina la correcta clasificación del texto.

Uno de estos métodos es LLSF: Linear Least-Square Fit. En él, existen dos vectores asociados a los documentos:

- I(dj), de largo |T|, y que representa a los términos
- y O(dj), de largo |C|, y que representa a las categorías. Es de tipo binario para entrenamiento y no binario para prueba.

Este procedimiento trata de determinar O(dj) dado I(dj), y construir una matriz M con |C| filas y |T| columnas, tal que al hacer el producto cruz entre M e I(dj) se encuentre O(dj).

La matemática del método puede sonar complicada, pero no lo es: se calcula la matriz de los datos de entrenamiento calculando un “linear least-square fit” que minimice el error en la fórmula



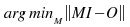
, donde minM(x)=M para el que x es mínimo



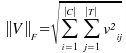
representa la llamada norma de Frobenius para una matriz |C|x|T|,

I es la matriz |T|x|Tr|, donde las columnas son los vectores de entrada para los documentos de entrenamiento; y O es la matriz |C|x|Tr|, donde las columnas son la salida de los vectores de entrenamiento.

M normalmente se calcula haciendo una descomposición valor singular en el conjunto de entrenamiento, y esta entrada genérica representa el grado de asociación entre la categoría ci y el término tk.

LLSF es considerado uno de los más efectivos clasificadores de textos, pero tiene el serio problema del costo computacional.