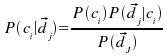
donde el espacio de eventos es el de los documentos, P(dj) es la probabilidad de escoger aleatoriamente un documento este esté representado por el vector d(j); y P(ci) es la probabilidad de que al tomar un documento cualquiera este pertenezca a la clase ci.
Estimar la probabilidad anterior no es fácil por lo complejo de dj; por lo que normalmente se asume que las variables que componen el documento vector son independientes; por lo que se puede representar la probabilidad anterior como:
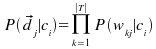
Dada esta suposición, es lo que se conoce como Ingenuo de Bayes (Naive Bayes), y por su simplicidad y rendimiento, es ampliamente utilizado en Categorización de Textos.
De todas las aproximaciones del Ingenuo de Bayes, la más común es la Independencia Binaria, donde se usan valores binarios para la representación del documento en el vector; pero se pueden encontrar otras variaciones que apuntan a:
- Relajar la restricción que el vector documento tenga valores binarios
- Introducir normalización en el largo del documento
- Relajar la suposición de independencia

No hay comentarios.:
Publicar un comentario